[딥러닝] 은닉층 활성화 함수, 손실함수, 경사하강법 종류

<은닉층 활성 함수>

1. 시그모이드 함수 

 1/ ( 1+ np.exp(-z)) 

장점 : 입력값에 어떤값을 넣어도 0 ~ 1사이 값이 나옴

단점 : z값이 0에서 멀어질수록, 경사가 없어진다. 

신경망 - 경사하강법 사용 - 경사가 0이면, 가중치와 편향이 업데이트가 안되서 학습이 매우 느려짐 

= 기울기 소실 문제 (vanishing gradient problem)

 

2. tanh 함수 

np.exp(z) - np.exp(-z) / np.exp(z) + np.exp(-z) 

장점 : 입력값에 어떤값을 넣어도 -1 ~ 1사이 값이 나옴

단점 : 기울기 소실 문제 (시그모이드와 큰 차이 없음) 

 

3. ReLu 

max(0, z) 

z < 0 : 기울기 항상 0 

z > 0 : 기울기 항상 1 

장점 : 기울기 소실 문제 덜 일어남, 성능 good, 경사 계산이 훨씬 빠름(경사가 0 or 1), 은닉층 활성화 함수로 가장 많이 사용 

 

4. Leaky ReLu 

 

<출력층 활성 함수>

1. 시그모이드 = 이중 분류 

: 아웃풋 0 ~ 1 -> 분류할 때 확률적인 판단 가능 

: 확률을 모두 더하면 1이 넘어가 버린다. 

 

2. softmax = 다중 분류 

: z값 계산 -> e^z값 계산 -> e^z / 전체 e^z들의 합 

:확률의 합 항상 1

: e^ i번째 뉴런의 z값 / 모든 뉴런의 e^z값 

 

3. 선형함수 = 회귀 문제 

: z값을 그대로 예측값으로 사용 ex) 집값 

 

<손실함수> 

1. 회귀 문제 = > 평균 제곱 오차 

J(W) = (1/2m) * np.sum{(hwx - y) ** 2 }

y(i) = i번째 데이터의 실제값 

x(i) = i번째 데이터의 입력변수 

hw(x(i)) = i번째 데이터의 예측값 

 

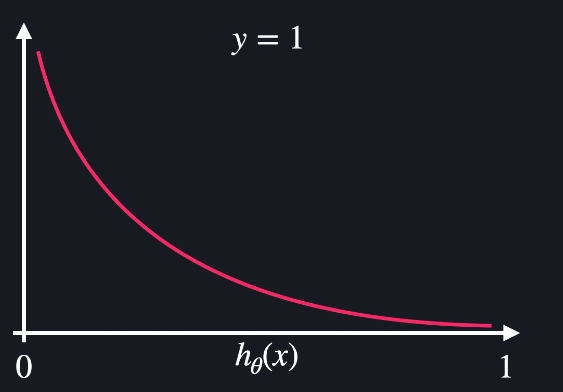
2. 이분적 분류 => 크로스 엔트로피 (로그 손실) 

J(W) = -(1/m) * np.sum((Y*np.log(hw(X) ) + ((1-Y) * np.log(1-hw(X)))

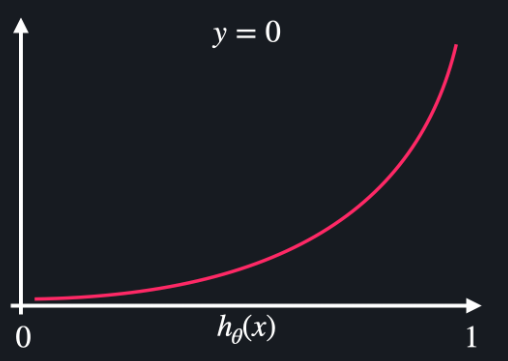
y=1 일때 손실함수 / y=0일때 손실함수 

3. 다중분류 => 크로스엔트로피 (로그손실)

: 비슷하긴 한데, 분류 종류가 여러개 여서 여러개를 다 로그값 안에 넣어준다. 

= 실제 분류 데이터 빼고 다 사라짐 

J(W) = -(1/m)* np.sum(np.sum(Y * np.log(hw(X))

 

<경사하강법>

1. 배치(batch)경사하강법

: 한번 경사 하강을 할때 모든 학습 데이터 사용 

-> 시간이 너무 오래 걸림 

 

2. 확률적 경사 하강법

(stocastic gradient descent) 

: 한번 경사 하강을 할때 임의로 하나의 데이터만 사용 

-> 하강을 하는 방향이 가장 빨리 내려오는 방향이 아닐 수 있음 

-> 국소점 주변에서도 수렴하지 않고 맴돌 수 있음

내려오는 방향을 정할때 배치 경사하강법은 모든 데이터를 고려해서 천천히 방향을 결정하는 반면, 확률적 경사하강법은 빠르게 국소점을 향해서 이동한다. 

 

3. 미니배치 경사하강법

: 학습데이터를 같은 크기의 여러 데이터셋으로 만듦 

= 한번 경사하강법을 할때, 만들어둔 하나의 데이터셋(작은 배치)를 사용

 

 *  대부분 미니 배치 경사 하강법 사용